读《算法导论》--排序算法

发表于 | 分类于 | | 阅读次数

读《算法导论》–排序算法

直观感受排序算法

http://www.sorting-algorithms.com/,

所有代码参考：

https://github.com/fsxchen/Algorithms_Python

插入排序与冒泡排序

插入排序

​ 对于插入排序法，最形象的解释就是下面这幅图片。

插入法的主要思想是：遍历一个数组，将遍历的那个数（key）放入到已经排好的数组中。

1
2
3
4
5
6
7
8
9
10
11
INSERT-SORT(A)
    for j = 2, to A.length
    key = A[j]
    i = j - 1
    while i > 0 and A[i] > key	//key要比当前的对比要大，那么就需要把当前的i往后移动
        A[i+1] = A[i]
        i = i -1
	// 执行完wihle之后，i后面这个坑就留给了key
	//为什么是i，应为A[i] > key 不成立，所以应该放在i+1这个坑
    A[i+1] = key

冒泡排序

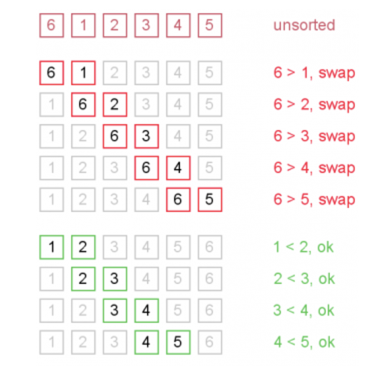
冒泡排序的思想就比较简单，遍历序列，然后用这个数和后面所有的来比较，如果这个书比较小，那么就交换位置。

1
2
3
4
5
MAOPAO-SORT(A)
    for j = 1, to A.length
        for i = j + 1, to A.length
            if A[j] > A[i]
	        exchange(A[i], A[j])

代码演示

https://github.com/fsxchen/Algorithms_Python

分析

对于这两个遍历法排序，时间复杂度都是$O(n^2)$,对于冒泡法，已经没有比较好的方法，因为不管怎样，都是需要遍历的，然后对于插入法排序，还是可以分析一下。

  • 如果将要处理的序列是从小到大已经排好序的？

    $O(n)$

  • 如果是从大到小排好的

    $O(n^2)$

堆排序

（二叉）堆是一个数组，可以近似看成一个完全二叉树。除了底层之外，其他层是完全充满的。

对于一个数组A,A.heap-size表示堆的长度，A.length表示数组长度

1
2
3
4
5
6
7
def PARRENT(i):
	return i/2
def LEFT (i):
	return 2i
def RIGHT:
	return 2i + 1

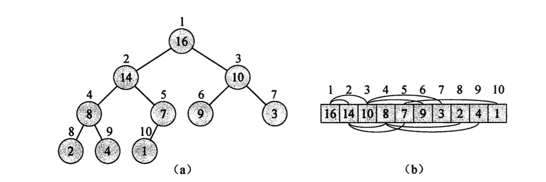
最小堆／最大堆是指A[PARRENT(i)] <=/>= A[i]

堆性质的维护

当向一个堆中加入一个数据的时候，如何维护

伪代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
MAX-HEAPIFY(A, i):
	left = LEFT(i)
	right = RIGHT(i)
	if l <= A.heap-size and A[l] > A[i]  // 左边的值大于当前节点
		largest = l
	else:
		largest = i                       //注意。这里是记录了当前最大的下标、下标、下标
	if r<= A.heap-seizs and A[r] > A[largest]
		largest = r
	if r != i:
		exchange A[i], A[largest]
		MAX-HEAPIFY(A, largest)

建堆

​ 这里需要注意的是，如果把一个长度为n的数组转化成为一个最大堆，也就是说A.length==A.heap-size那么其叶结点的下标为n/2 + 1, ...n!，这里下标是从1开始！

1
2
3
BUILD-M-HEAP(A):
	for i = A.length／2 downto 1
		MAX-HEAPIFY(A, i)

​ 考虑到这个是自底向上的建堆的方式，从低层，每次都进行一次堆最大性质的维护。那么可以保证该堆是一个最大堆。

堆排序算法

1
2
3
4
5
6
SORT-HEAP(A):
	BUILD-M-HEAP(A)
	for i = A.length downto 2:
		exchange A[1] with A[i]
		A.heap-size = A.heap-size-1
		MAX-HEAPIFY(A, 1)

代码演示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#!/usr/bin/python
#coding:utf-8
def PARRENT(i):
    return int(i/2)
def LEFT(i):
    return 2 * i + 1
def RIGHT(i):
    return 2 * i + 2
def MAX_HEAPIFY(A, i, heap_size=None):
    l = LEFT(i)
    r = RIGHT(i)
    if heap_size is None:
        heap_size = len(A) - 1
    else:
        heap_size -= 1
    if l <= heap_size and A[l] > A[i]:
        largest = l
    else:
        largest = i
    if r <= heap_size and A[r] > A[largest]:
        largest = r
    if largest != i:
        # print "Exchage %d and %d" %(i, largest)
        A[i], A[largest] = A[largest], A[i]
        MAX_HEAPIFY(A, largest, heap_size)
def BUILD_MAX_HEAP(A):
    for i in range(int(len(A))/2, -1, -1):
        MAX_HEAPIFY(A, i)
def HEAPSORT(A):
    BUILD_MAX_HEAP(A)
    heap_size = len(A)
    print "The MAX_HEAPIFY is", A
    for i in range((len(A) - 1), 0, -1):
        A[0], A[i] = A[i], A[0]
        heap_size -= 1
        MAX_HEAPIFY(A, 0, heap_size)

堆的应用-优先队列

优先队列是一种用来维护由一组元素构成的集合S的数据结构，支持

  • INSERT(S, x)：把元素x插入到集合S中
  • MAXIMUM(S)：返回S中具有最大键字的元素
  • EXTRACT-MAX(S)：去掉并返回具有最大键字的元素
  • INCREASE-KEY（S, x, k)：将元素x的关键字值增加到k

如何使用堆来实现优先队列

快速排序

核心思想就是归并排序

  • 分解： 数组A[p, r]将被划分为两个（可能为空）的子数组A[p..q-1]和A[q+1, r]，使得A[p..q-1]中的每一个元素都小于A[q]，A[q+1, r]中的每一个元素都大于A[q]
  • 解决：通过递归来对子数组来排序
  • 合并：不需要合并操作
1
2
3
4
5
QUICK-SORT(A, p, r)
	if p < r:
		q = PARTITION(A, p, r)
		QUICK-SORT(A, p, q - 1)
		QUICK-SORT(A, q+1 ,r)

关键部分在于PARTITION这个函数

1
2
3
4
5
6
7
8
9
PARTITION(A, p, r):
	x = A[r]	//取用最后一个数来分隔
	i = p - 1		//i是来跟踪第几个比x小
	for j = p to r -1:
		if A[j] <= x:
			i = i + 1
			exchange A[i] with A[j]
	exchange A[i+1] with A[r]
	return i+1

快速排序的随机化版本

1
2
3
4
RANDOMIZED-PARTITON(A, p, r):
	i = RANDOM(p, r)
	exchange A[i], A[r]
	return PARTITION(A, p, r)

快速排序的优势很明显，首先在时间上，其时间复杂度为$nlgn$，其次，不会占用额外的空间，属于原址排序，节省空间，是一种运用最广泛的排序算法。

线性时间排序

任何比较排序法所用的时间最短为$nlgn$

基数排序

只应用与卡片打孔的机器

桶排序

中位数和顺序统计量

最小值和最大值

1
2
3
4
5
MAXIMUM(A):
	max = A[1]
	for i = 2 ro A.length
		if max < A[i]:
			max = A[i]

当想要获取一个序列中的一个最大值或者是最小值的时候，可以看到时间复杂度为$n$

同时找到最大值和最小值

理论上来讲，最大值需要一次比较，最小值需要一次，一共需$2(n-1)$比较。如果在每个元素之间比较，然后小值和最小值比较，大的和最大值比较，只需要比较3*n/2次

找到第i小／大的元素

1
2
3
4
5
6
7
8
9
10
11
RANDOMZIED-SELECT(A, p, r):
	if p == r
		return A[p]
	q = RANDOMIZED-PARTITION(A, p, r, i)
	k = p - q + 1
	if i == k
		return A[q]
	else if i < k   //那么要找的就在左边
		return RANDOMZIED-SELECT(A, p, q-1, i)
	else
		return RANDOMZIED-SELECT(A, q+1, r, i -k)
坚持技术分享，您的支持将鼓励我继续创作！