深度学习
Logistic 函数
Logistic函数或Logistic曲线是一种常见的S形函数,它是皮埃尔·弗朗索瓦·韦吕勒在1844或1845年在研究它与人口增长的关系时命名的。广义Logistic曲线可以模仿一些情况人口增长(P)的S形曲线。起初阶段大致是指数增长;然后随着开始变得饱和,增加变慢;最后,达到成熟时增加停止。[1]
很像一个“S”型吧,所以又叫 sigmoid曲线(S型曲线)。阶跃函数(激活函数)
$$
y=\sigma(z)
$$
$\sigma$ 的定义为
$$
\sigma={1\over 1+e^{-z}}
$$
python实现Logistic函数
|
|
Logistic函数的导数
|
|
Logistic回归
logistic回归是一种广义线性回归(generalized linear model),因此与多重线性回归分析有很多相同之处。它们的模型形式基本上相同,都具有 $w‘x+b$,其中w和b是待求参数,其区别在于他们的因变量不同,多重线性回归直接将w’x+b作为因变量,即y =w‘x+b,而logistic回归则通过函数L将w‘x+b对应一个隐状态p,p =L(w‘x+b),然后根据p 与1-p的大小决定因变量的值。如果L是logistic函数,就是logistic回归,如果L是多项式函数就是多项式回归。
训练一个Logistic回归训练器
|
|
Softmax
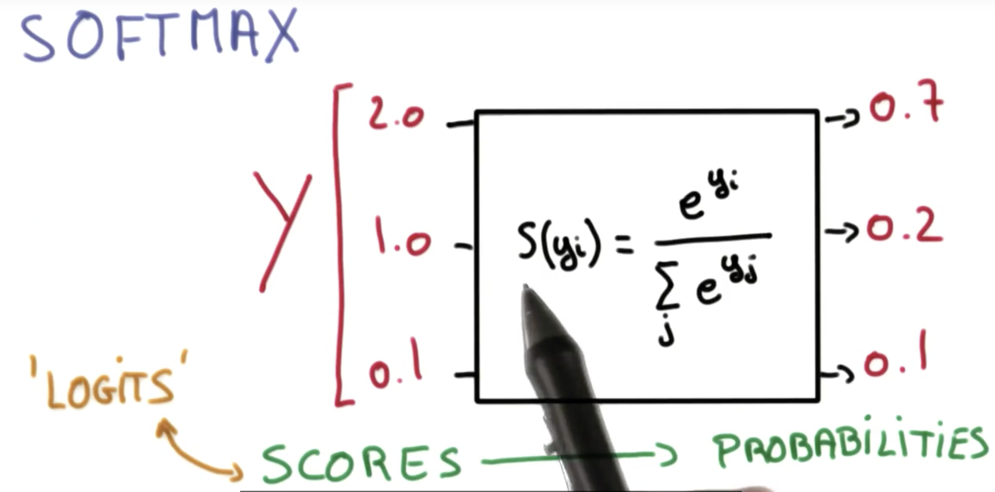
|
|
One-hot 编码
损失函数
交叉熵
训练集合
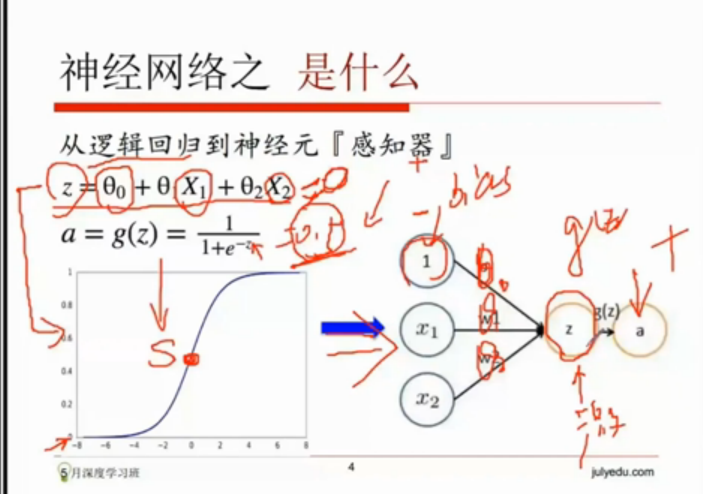
多层神经网络
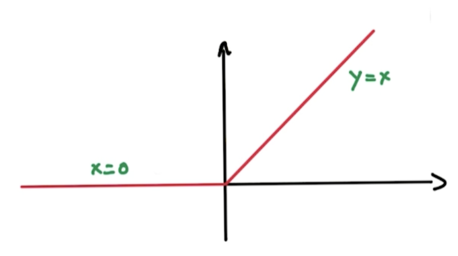
一个常用的非线性函数叫 ReLU(rectified linear unit))。ReLU 函数对所有负的输入,返回 0;所有 x>0 的输入,返回 x。
隐藏层用 ReLU 作为激活函数
- 最简单的非线性函数
Tensorflow的解决问题步骤
- 1、先定义模型的整体图结构,未知的部分,比如输入就用placeholder来代替。
- 2、再定义最后与目标的误差函数。
- 3、最后选择优化方法。

