回归

连续监督学习

• 连续输出和离散输出的区别

这里的连续主要是指输出是连续的

回归线性方程

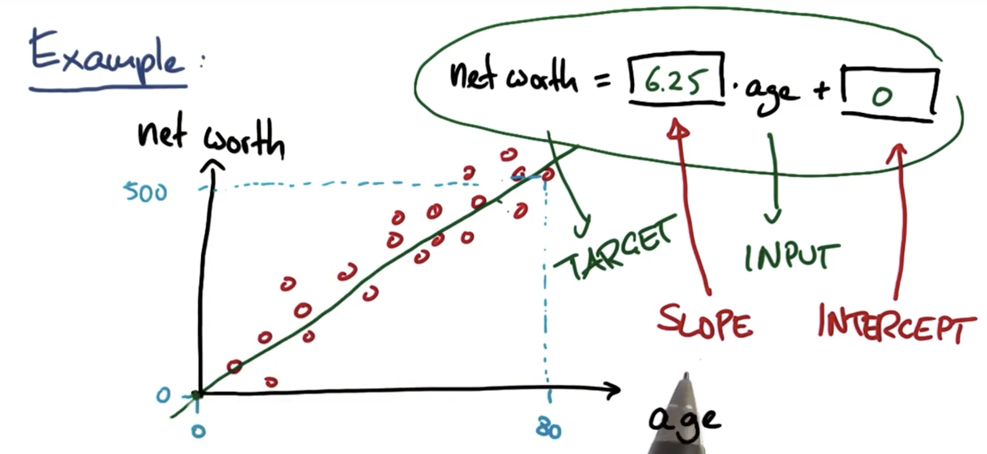
slope：斜率
intercept：截距

斜率和截距

斜率越大，上升越快

Sklearn中的线形拟合

>>> from sklearn import linear_model
>>> reg = linear_model.LinearRegression()
>>> reg.fit ([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
>>> reg.coef_
array([ 0.5,  0.5])

线性回归误差

使误差有最小值。

最小二乘法（OLS）

sklearn中的线性拟合即使用的是该方法

import numpy as np
import matplotlib.pyplot as plt

dots = np.array([[1,6], [2,5], [3,7], [4,10], [5, 12]])

X = dots[:, 0]
Y = dots[:, 1]
plt.scatter(X, Y, color = "b", label="fast")


def nihe(k, x, b):
    return k*x + b


#a0 = （∑Yi) / n - a1（∑Xi) / n （式1-8)
#a1 = [n∑Xi Yi - （∑Xi ∑Yi)] / [n∑Xi2 - （∑Xi)2 )] （式1-9)

n = dots.shape[0]
a1 = (n*sum(X*Y) - sum(X)*sum(Y)) / (n*sum(X**2)-(sum(X)**2))
a0 = sum(Y)/n - a1*(sum(X))/n
print(a0, a1)

R_Y = [nihe(a1, x, a0) for x in X]
plt.plot(X, R_Y)
plt.show()

使用平方误差和来评估拟合的效果？

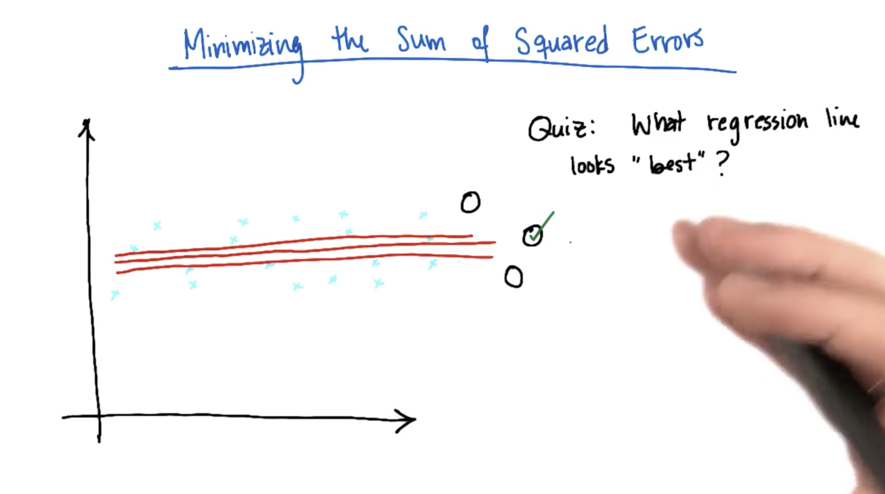
​ 如上图所示，如果只是使用绝对值，那么途中的3种拟合方式没有什么区别，然而如果使用平方的方式，只有中间的误差是最小的。

• 使用平方误差和的方式的不足只处
  

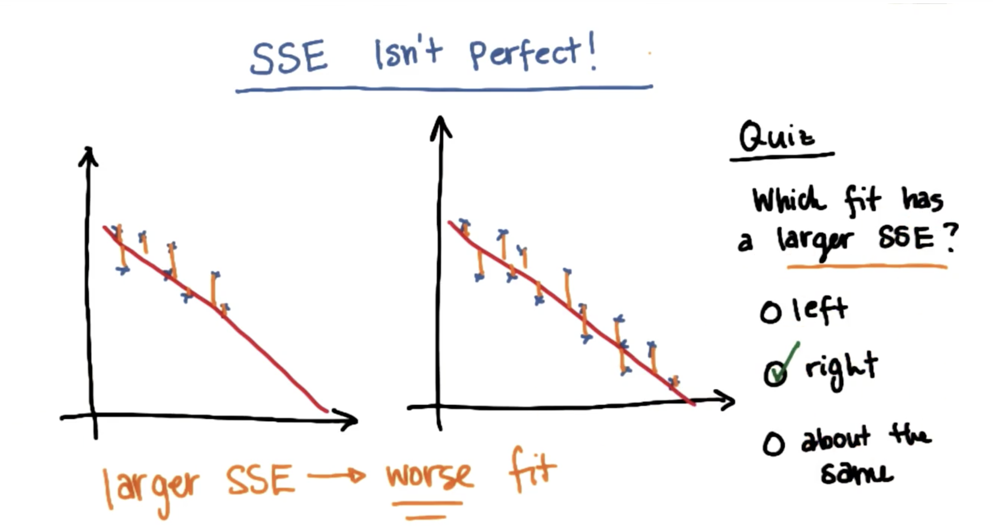
R平方指标

R平方指标弥补了平方误差和的不足之处。

梯度下降法

什么数据适用于线性回归

线性的，可以拟合成
$$
y = ax + b
$$

回归于分类的比较

比较	监督分类	回归
输出类型	离散（类型标签）	连续（数字）
目的	找到决策边界	最优拟合线
评估指标	准确率	R平方值

多变量（多元）回归（MULTI-VARIATE REGRESSION)